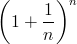- Число Пі
- Число e (число Ейлера)
- Число Фі. Золотий перетин (стаття з журналу "Наука и жизнь", автор Виктор Лаврус)
- Числові піраміди (цікаво)
- Число 37
- ВВС. Математика. Музыка простых чисел. (3 фильма)
ВВС. Музыка простых чисел. Фильм 1.
Число 37 обладает многими любопытными свойствами. Так, умноженное на 3 и на числа, кратные 3 (до 27 включительно), оно дает произведения, изображаемые одной какой-либо цифрой:
37 × 3 = 111;
37 × 6 = 222;
37 × 9 = 333;
37 × 12 = 444;
37 × 15 = 555;
37 × 18 = 666;
37 × 21 = 777;
37 × 24 = 888;
37 × 27 = 999.
Произведение от умножения 37 на сумму его цифр равняется сумме кубов тех же цифр, т. е.:
37 × (3 + 7) = 3^3 + 7^3 = 370.
Если в числе 37 взять сумму квадратов его цифр и вычесть из этой суммы произведение тех же цифр, то опять получим 37:
(3^2 + 7^2) – 3×7 = 37.
Но едва ли не самым интересным свойством числа 37 является то, что некоторые кратные ему числа при круговой перестановке входящих в них цифр дают опять-таки числа, кратные 37. Например:
259 = 7 × 37
592 = 16 × 37
925 = 25 × 37
То же самое верно относительно чисел 185, 518, 851 и чисел 296, 629, 962. Все эти числа состоят из тех же цифр, только переставляемых в круговом порядке, и все они кратны 37.
Подобным же свойством отличаются и некоторые числа, кратные 41. Так, числа:
17589; 75891; 58917; 89175 и 91758,
как легко проверить, все кратны 41, и каждое получается из предыдущего путем только одной круговой перестановки входящих в число цифр.
Источник — «Пять минут на размышление». Москва 1950. Книга составлена по материалам Л. Успенского, А. Студенцова, Я. Перельмана, Игнатьева и др.
Науковці, художники й архітектори вважають число Фі самим красивим у всесвіті ...
А чому так прочитайте ці публікації про число Фі та про золотий перетин.
Число Фі також відоме як золотий перетин, Ф — важливий математичний об’єкт, і записується він як 1,6180339887… Фі — це результат вирішення квадратного рівняння, але являє собою геометричну конструкцію. Золотий перетин виникає при діленні безперервної величини на дві частини таким чином, що менша частина так відноситься до більшої, як велика до всієї величини.
(а + с)/с = с/а = Ф
Завдяки своїм унікальним властивостям, Ф використовується в мистецтві та архітектурі. У художників епохи Відродження це число вважалося Божественною пропорцією.
Читати ще за темою:
Божественная Пропорция: Нерасшифрованный Код
Числа Фибоначчи в природе
Золотое сечение. Взгляд сквозь века
Відео :
Не можу обійти стороною роман Дена Брауна «Код да Вінчі». Цей роман купила, як тільки він був надрукований російською мовою, ще не знала про що він. Але мою увагу привернула назва. А це тому, що я преклоняюся перед геніальністю великої людини – художника та винахідника – Леонардо да Вінчі. Прочитала, не відриваючись. Я не збираюся переказувати її теософський (релігійний) замисел та оцінювати художню та літературну цінність. Мене вразила кількість загадок, на які автор дає свої оригінальні відповіді-розгадки. Знайшла в мережі презентацію і не утримуюся, щоб її не показати … Цю чудову презентацію створено учнями із Томську.
У мене накопичилася велика кількість матеріалів на дану тему - "Піраміди і число Ф", "Музика і золотий перетин" та ін. Так що далі буде.
Число Пі
Число π— математична константа, що визначається у Евклідовій геометрії як відношення довжини кола до його діаметра
або як площа круга одиничного радіуса.
Довжина кола дорівнює π, якщо його діаметр 1.
Число π виникло в геометрії як відношення довжини кола до довжини його діаметра, проте воно з'являється і в інших областях математики. Вперше позначенням цього числа грецькою літерою π скористався британський математик Джонс (1706), а загальноприйнятим воно стало після робіт Ейлера. Це позначення походить від початкової букви грецьких слів περιφέρεια — оточення, периферія та περίμετρος — периметр.
Цікавий факт: саме точне значення числа Пі для свого часу отримав Платон (в деяких публікаціях Архімед), прийшовши до досить простої формули
Цікава особливість: Як відомо, Єгипетські піраміди — це гробниці фараонів. Їх було споруджено в третьому тисячолітті до н.е. Найбільші дві єгипетські піраміди — це піраміда Хеопса (висота — 146 м, периметр основи — близько 1 км) і піраміда Хефрена (висота — 143 м).
Якщо довжину обводу основи піраміди Хеопса поділити на її подвоєну висоту, то вийде 3,14159 — число Пі з точністю до шостого знаку.
Цікавий факт: незважаючи на відносно рідкісне використання числа Пі, воно є найвідомішою у світі математичної константою. Повне значення числа Пі ще не вдавалося вирахувати. Примітно, що число Пі і сам символ його позначення використовується в математичному світі вже більше 250 років.
Цікавий факт: хоча число Пі використовується в офіційній математиці не більше 250 років, вперше воно було згадано близько 1650 до нашої ери в Єгипті, переписувачем Ахмес. На даний момент документ із згадкою цього числа називають числом Ахмеса або Ринда. У цілому, число Пі вивчається людьми більше 4 тисяч років.
Цікавий факт: найбільш точне значення числа Пі в середні століття мав Леонардо да Вінчі і Дюрер Альберт. Вони працювали над обчисленням квадратури кола. Округлене значення в 3,14 мало для них певне значення. Після них, найбільше наблизився до числа Пі ніхто інший як Ісаак Ньютон, який розрахував його до 16 знаків.
Першим запровадив символ e Леонард Ейлер. Йому належить так багато відкриттів, пов’язаних з числом e, що зрештою число e стали називати «числом Ейлера».
Також число e називають числом Непера. Джон Непер – шотландський математик. Самого числа він не згадував, натомість збудував на його основі таблиці логарифмів. Одночасно кандидатами в автори константи вважаються Якоб Бернуллі, Лейбніц, Гюйгенс.
Як і π, е – трансцендентне число, ці числа не можна виразити за допомогою дробів та коренів, вони не можуть бути коренями якогось алгебраїчного рівняння з раціональними коефіцієнтами.
Число е у довкіллі. Радіоактивність полонію-210 зменшується в e разів за середній час життя одного атому, а раковина молюску Nautilus – це графік степенів e, який обернено навколо вісі.
Число е зустрічається і там, де довкілля завідомо не до чого. Банк, який обіцяє своїм вкладникам 1% на рік, за 100 років збільшує вклад в е разів. Для 0,1% і 1000 років результат ще більше наближується до константи е. Якоб Бернуллі, знавець і теоретик азартних ігор, саме так довів е, коли обмірковував скільки заробляють лихварі (рос. ростовщики).
Припустимо, що хтось поклав 1$ у банк, який сплачує 4% річних. Якщо відсотки складні, то після кожного їх нарахування кількість грошей збільшуватиметься і відсотки кожного наступного разу нараховуватимуться від збільшеної загальної суми. Чим частіше робитимуть перерахунки, тим швидше збільшуватиметься вклад. Коли щороку нараховувати складні відсотки, 1$ за 25 років перетвориться у (1 + 0,04)25, тобто у 2,66$. Коли нараховуватимуть складні відсотки кожні півроку, то за 25 років долар перетвориться у (1 + 0,02)50, або 2,69$.
У рекламних проспектах банків їх автори особливо підкреслюють, скільки разів на рік нараховуються відсотки. Може скластися враження, що коли досить часто нараховувати відсотки (наприклад, мільйон разів на рік), то за 25 років долар перетвориться у досить велику суму грошей. Насправді ж цього не відбудеться. Через 25 років долар виріс би до величини
де n — кількість нарахувань прибутку. При n, що прямує до
нескінченності, цей вираз прямуватиме до границі, яка дорівнює 2,718…,
що лише на 3 центи більше за ту суму, яку б отримали, коли б прибуток
нараховувався один раз кожні півроку. Ця границя і називається числом е.
Перші 20 знаків числа е такі:
Цікавий факт: саме точне значення числа Пі для свого часу отримав Платон (в деяких публікаціях Архімед), прийшовши до досить простої формули
Цікава особливість: Як відомо, Єгипетські піраміди — це гробниці фараонів. Їх було споруджено в третьому тисячолітті до н.е. Найбільші дві єгипетські піраміди — це піраміда Хеопса (висота — 146 м, периметр основи — близько 1 км) і піраміда Хефрена (висота — 143 м).
Цікавий факт: незважаючи на відносно рідкісне використання числа Пі, воно є найвідомішою у світі математичної константою. Повне значення числа Пі ще не вдавалося вирахувати. Примітно, що число Пі і сам символ його позначення використовується в математичному світі вже більше 250 років.
Цікавий факт: хоча число Пі використовується в офіційній математиці не більше 250 років, вперше воно було згадано близько 1650 до нашої ери в Єгипті, переписувачем Ахмес. На даний момент документ із згадкою цього числа називають числом Ахмеса або Ринда. У цілому, число Пі вивчається людьми більше 4 тисяч років.
Цікавий факт: найбільш точне значення числа Пі в середні століття мав Леонардо да Вінчі і Дюрер Альберт. Вони працювали над обчисленням квадратури кола. Округлене значення в 3,14 мало для них певне значення. Після них, найбільше наблизився до числа Пі ніхто інший як Ісаак Ньютон, який розрахував його до 16 знаків.
Цікавий
факт: число Пі називають мінімум трьома позначеннями. Перше –
кругова постійна, друге – константа Архімеда і останнє, число
Лудольфа. Звичайно, не враховуючи самого поширеного – число Пі.
Цікавий факт: перші 144 цифри після коми в числі Пі закінчуються трьома шістками (666). Це згадано в Біблії як число звіра.
Цікавий факт: перші 144 цифри після коми в числі Пі закінчуються трьома шістками (666). Це згадано в Біблії як число звіра.
Цікавий факт: японець Гото Хірюкі зміг відтворити в розумі більше 42 тисяч цифр числа Пі після коми в 1995 році. Донині цей чоловік є чемпіоном в області запам'ятовування числа Пі.
Цікавий факт: людство ніколи не зможе з точністю вирахувати площу круга й довжину кола, так як не знає повне і точне значення числа Пі.
Цікавий факт: у числа Пі є навіть свій день – 14 березня кожного року. Цей день присвячений Пі завдяки схожості – 3 місяць 14 число. У математиків навіть існує традиція, починати святкування в 1:59, щоб як можна точніше дотриматися пропорції.
До речі, в цей день народився Альберт Енштейн, засновник теорії відносності.
УВАГА!!! Якщо Вам цікаво дізнатися, починаючи з якої позиції в десятковому запису числа π вперше зустрінеться дата вашого народження, зайдіть на сайт «Математические этюды», у розділі «Миниатюры» знайдіть «Нормальность числа π».
УВАГА!!! Якщо Вам цікаво дізнатися, починаючи з якої позиції в десятковому запису числа π вперше зустрінеться дата вашого народження, зайдіть на сайт «Математические этюды», у розділі «Миниатюры» знайдіть «Нормальность числа π».
Число e (число Ейлера)
Число е зустрічається у шкільному курсі рідше, ніж число Пі, та у вищій математиці воно відіграє важливу роль і зустрічається дуже часто.Першим запровадив символ e Леонард Ейлер. Йому належить так багато відкриттів, пов’язаних з числом e, що зрештою число e стали називати «числом Ейлера».
Також число e називають числом Непера. Джон Непер – шотландський математик. Самого числа він не згадував, натомість збудував на його основі таблиці логарифмів. Одночасно кандидатами в автори константи вважаються Якоб Бернуллі, Лейбніц, Гюйгенс.
Як і π, е – трансцендентне число, ці числа не можна виразити за допомогою дробів та коренів, вони не можуть бути коренями якогось алгебраїчного рівняння з раціональними коефіцієнтами.
Число е у довкіллі. Радіоактивність полонію-210 зменшується в e разів за середній час життя одного атому, а раковина молюску Nautilus – це графік степенів e, який обернено навколо вісі.
Число е зустрічається і там, де довкілля завідомо не до чого. Банк, який обіцяє своїм вкладникам 1% на рік, за 100 років збільшує вклад в е разів. Для 0,1% і 1000 років результат ще більше наближується до константи е. Якоб Бернуллі, знавець і теоретик азартних ігор, саме так довів е, коли обмірковував скільки заробляють лихварі (рос. ростовщики).
Припустимо, що хтось поклав 1$ у банк, який сплачує 4% річних. Якщо відсотки складні, то після кожного їх нарахування кількість грошей збільшуватиметься і відсотки кожного наступного разу нараховуватимуться від збільшеної загальної суми. Чим частіше робитимуть перерахунки, тим швидше збільшуватиметься вклад. Коли щороку нараховувати складні відсотки, 1$ за 25 років перетвориться у (1 + 0,04)25, тобто у 2,66$. Коли нараховуватимуть складні відсотки кожні півроку, то за 25 років долар перетвориться у (1 + 0,02)50, або 2,69$.
У рекламних проспектах банків їх автори особливо підкреслюють, скільки разів на рік нараховуються відсотки. Може скластися враження, що коли досить часто нараховувати відсотки (наприклад, мільйон разів на рік), то за 25 років долар перетвориться у досить велику суму грошей. Насправді ж цього не відбудеться. Через 25 років долар виріс би до величини
Перші 20 знаків числа е такі:
е ≈ 2,71828182845904523536.
